Главная / Решить вариант ОГЭ
Решить вариант ОГЭ по математике 2026
Для загрузки этого же теста в случае перезагрузки страницы (а также для сохранения статистики набранных баллов в личном кабинете) - пожалуйста, войдите или зарегистрируйтесь. Регистрация займет не больше минуты.
СПРАВОЧНЫЕ МАТЕРИАЛЫ
(их дадут на ОГЭ: зубрить их не надо, но ориентироваться в них - надо)
АЛГЕБРА
-
Формула корней квадратного уравнения:
$$x=\frac{-b\pm\sqrt{D}}{2a}\text{, где } D=b^2-4ac.$$
-
Если квадратный трёхчлен $$ax^2+bx+c$$ имеет два корня: $$x_1$$ и $$x_2$$, то
$$ax^2+bx+c=a(x-x_1)(x-x_2)$$;если квадратный трёхчлен $$ax^2+bx+c$$ имеет единственный корень $$x_0$$, то$$ax^2+bx+c=a(x-x_0)^2$$.
-
Абсцисса вершины параболы, заданной уравнением $$ax^2+bx+c$$ :
$$x_0=-\frac{b}{2a}.$$
-
Формула n-го члена арифметической прогрессии ($$a_n$$), первый член которой равен $$a_1$$ и разность равна $$d$$:
$$a_n=a_1+d(n-1)$$.
-
Формула суммы первых n членов арифметической прогрессии:
$$S_n=\frac{(a_1+a_n)n}{2}$$.
-
Формула n-го члена геометрической прогрессии $$b_n$$, первый член которой равен $$b_1$$, а знаменатель равен $$q$$:
$$b_n=b_1 \cdot q^{n-1}$$
-
Формула суммы первых $$n$$ членов геометрической прогрессии:
$$S_n=\frac{(q^{n}-1)b_1}{q-1}$$.
-
Формулы сокращенного умножения:
$$(a+b)^2=a^2+2ab+b^2$$;$$(a-b)^2=a^2-2ab+b^2$$;$$a^2-b^2=(a-b)(a+b)$$.
-
Свойства арифметического квадратного корня:
$$\sqrt{ab}=\sqrt{a}\cdot\sqrt{b} \text{ при } a\geq0, b\geq0$$;$$\sqrt{\frac{a}{b}}=\frac{\sqrt{a}}{\sqrt{b}} \text{ при } a\geq0, b>0$$.
-
Свойства степени при a>0, b>0
$$a^{-n} = \frac{1}{a^n}$$;$$a^n \cdot a^m = a^{n+m}$$;$$\frac{a^n}{a^m} = a^{n-m}$$;$$\Big(a^n\Big)^m = a^{nm}$$;$$(ab)^n = a^n \cdot b^n$$;$$\bigg(\frac{a}{b}\bigg)^n = \frac{a^n}{b^n}$$.
Таблица квадратов двузначных чисел
| Единицы | |||||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ||
Десятки | |||||||||||
| 1 | 100 | 121 | 144 | 169 | 196 | 225 | 256 | 289 | 324 | 361 | |
| 2 | 400 | 441 | 484 | 529 | 576 | 625 | 676 | 729 | 784 | 841 | |
| 3 | 900 | 961 | 1024 | 1089 | 1156 | 1225 | 1296 | 1369 | 1444 | 1521 | |
| 4 | 1600 | 1681 | 1764 | 1849 | 1936 | 2025 | 2116 | 2209 | 2304 | 2401 | |
| 5 | 2500 | 2601 | 2704 | 2809 | 2916 | 3025 | 3136 | 3249 | 3364 | 3481 | |
| 6 | 3600 | 3721 | 3844 | 3969 | 4096 | 4225 | 4356 | 4489 | 4624 | 4761 | |
| 7 | 4900 | 5041 | 5184 | 5329 | 5476 | 5625 | 5776 | 5929 | 6084 | 6241 | |
| 8 | 6400 | 6561 | 6724 | 6889 | 7056 | 7225 | 7396 | 7569 | 7744 | 7921 | |
| 9 | 8100 | 8281 | 8464 | 8649 | 8836 | 9025 | 9216 | 9409 | 9604 | 9801 | |
ГЕОМЕТРИЯ
- Сумма углов выпуклого n-угольника равна $$ 180^o (n-2) $$.
-
Средняя линия треугольника и трапеции
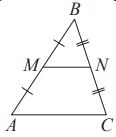
MN - ср. лин.MN || AC$$MN = \frac{AC}{2}$$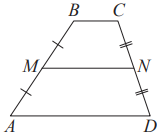
BC || ADMN - ср. лин.MN || AD$$MN = \frac{BC + AD}{2}$$ -
Описанная и вписанная окружности правильного треугольника
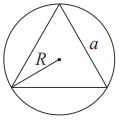
$$R = \frac{a\sqrt{3}}{3}$$$$S = \frac{a^2\sqrt{3}}{4}$$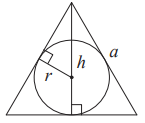
$$r = \frac{a\sqrt{3}}{6}$$$$h = \frac{a\sqrt{3}}{2}$$ -
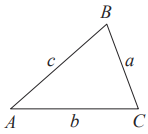
Для треугольника ABC со сторонами $$AB = c, AC = b, BC = a$$:$$\frac{a}{sinA} = \frac{b}{sinB} = \frac{c}{sinC} = 2R$$,где R – радиус описанной окружности.
Для треугольника ABC со сторонами $$AB = c, AC = b, BC = a$$:$$c^2 = a^2 + b^2 - 2ab\cos{C}$$. -
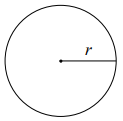
Длина окружности $$С = 2\pi r$$Площадь круга $$S = \pi r^2$$
-
Параллелограмм
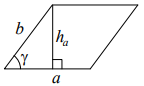
$$S=ah_a$$$$S=ab\sin{\gamma}$$Треугольник
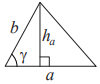
$$S=\frac{1}{2}ah_a$$
$$S=\frac{1}{2}ab\sin{\gamma}$$ -
Трапеция
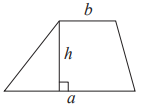
$$S=\frac{a+b}{2}\cdot h$$Ромб
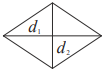
$$d_1, d_2$$ - диагонали$$S=\frac{1}{2}d_1d_2$$ -
Прямоугольный треугольник
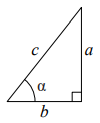
$$\sin{\alpha} = \frac{a}{c}$$
$$\cos{\alpha} = \frac{b}{c}$$
$$tg\alpha = \frac{a}{b}$$ - Теорема Пифагора: $$a^2 + b^2 = c^2$$
- Основное тригонометрическое тождество: $$\sin^2{\alpha} + \cos^2{\alpha} = 1$$
-
Некоторые значения тригонометрических функций
$$\alpha$$ градусы 0o 30o 45o 60o 90o 180o 270o 360o $$sin{\alpha}$$ 0 $$\frac{1}{2}$$ $$\frac{\sqrt{2}}{2}$$ $$\frac{\sqrt{3}}{2}$$ 1 0 -1 0 $$cos{\alpha}$$ 1 $$\frac{\sqrt{3}}{2}$$ $$\frac{\sqrt{2}}{2}$$ $$\frac{1}{2}$$ 0 -1 0 1 $$tg{\alpha}$$ 0 $$\frac{\sqrt{3}}{3}$$ 1 $$\sqrt{3}$$ - 0 - 0
При выполнении работы пользуйтесь, пожалуйста, только бумагой, ручкой и линейкой (калькулятором на ОГЭ по математике пользоваться нельзя).
Часть 1
Ответом к заданиям 1-19 является число (положительное или отрицательное, целое или дробное, но обязательно в десятичном виде; если получилась обыкновенная дробь - запишите ее в виде десятичной.
На рисунке изображён план сельской местности. Таня на летних каникулах приезжает в гости к дедушке в деревню Антоновка (на плане обозначена цифрой 1). В конце каникул дедушка на машине собирается отвезти Таню на автобусную станцию, которая находится в деревне Богданово. Из Антоновки в Богданово можно проехать по просёлочной дороге мимо реки. Есть другой путь — по шоссе до деревни Ванютино, где нужно повернуть под прямым углом налево на другое шоссе, ведущее в Богданово. Третий маршрут проходит по просёлочной дороге мимо пруда до деревни Горюново, где можно свернуть на шоссе до Богданово. Четвёртый маршрут пролегает по шоссе до деревни Доломино, от Доломино до Горюново по просёлочной дороге мимо конюшни и от Горюново до Богданово по шоссе. Ещё один маршрут проходит по шоссе до деревни Егорка, по просёлочной дороге мимо конюшни от Егорки до Жилино и по шоссе от Жилино до Богданово. Шоссе и просёлочные дороги образуют прямоугольные треугольники. По шоссе Таня с дедушкой едут со скоростью 50 км/ч, а по просёлочным дорогам — со скоростью 30 км/ч. Расстояние от Антоновки до Доломино равно 12 км, от Доломино до Егорки — 4 км, от Егорки до Ванютино — 12 км, от Горюново до Ванютино — 15 км, от Ванютино до Жилино — 9 км, а от Жилино до Богданово — 12 км.
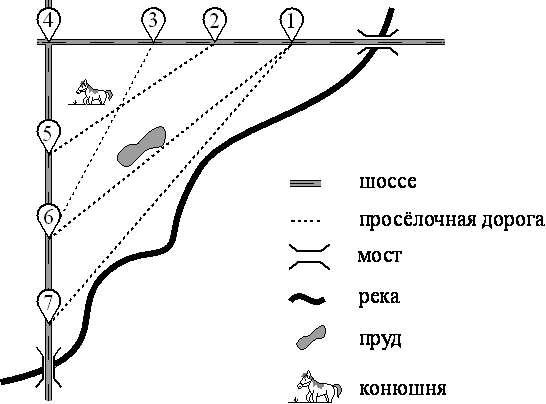
1
Пользуясь описанием, определите, какими цифрами на плане обозначены деревни.
Заполните таблицу, в бланк ответов перенесите последовательность четырёх цифр без пробелов, запятых и других дополнительных символов.
| Деревни | Егорка | Ванютино | Доломино | Жилино |
| Цифры |
Ответ:
2
Найдите расстояние от Антоновки до Егорки по шоссе. Ответ дайте в километрах.
Ответ:
3
Найдите расстояние от Доломино до Горюново по прямой. Ответ дайте в километрах.
Ответ:
4
Сколько минут затратят на дорогу Таня с дедушкой из Антоновки в Богданово, если поедут мимо пруда через Горюново?
Ответ:
5
На шоссе машина дедушки расходует 5,5 литра бензина на 100 км. Известно, что на путь из Антоновки до Богданово через Ванютино и путь через Егорку и Жилино мимо конюшни ей необходим один и тот же объём бензина. Сколько литров бензина на 100 км машина дедушки расходует на просёлочных дорогах?
Ответ:
6
Найдите значение выражения $$\frac{7^{-3} \cdot 7^{13}}{7^{8}}$$.
Ответ:
7
На координатной прямой отмечены числа x, y и z. Какая из разностей z - x, z - y, y - x отрицательна?

1) z-x
2) z-y
3) y-x
4) ни одна из них
8
Найдите значение выражения $$\sqrt{\frac{4x^2}{y^6}}$$ при x = 8 и y = 2.
Ответ:
9
Найдите корень уравнения 4(x - 6) = 5.
Ответ:
10
В лыжных гонках участвуют 11 спортсменов из России, 6 спортсменов из Норвегии и 3 спортсмена из Швеции. Порядок, в котором спортсмены стартуют, определяется жребием. Найдите вероятность того, что первым будет стартовать спортсмен из Норвегии или Швеции.
Ответ:
11
На рисунках изображены графики функций вида y = kx + b. Установите соответствие между знаками коэффициентов k и b и графиками функций.А) k<0, b<0
Б) k>0, b<0
В) k<0, b>0
В таблице под каждой буквой укажите соответствующий номер.
1) 

2) 

3) 

| А | Б | В |
12
В фирме «Эх, прокачу!» стоимость поездки на такси (в рублях) длительностью более 5 минут рассчитывается по формуле $$C=150+11(t - 5)$$, где $$t$$ — длительность поездки (в минутах). Пользуясь этой формулой, рассчитайте стоимость 12-минутной поездки. Ответ дайте в рублях.
Ответ:
13
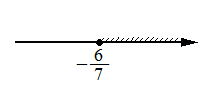
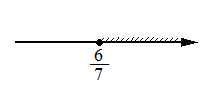
Укажите решение неравенства 49x2 ≥ 36.
1) 

2) 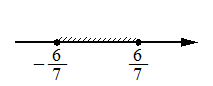
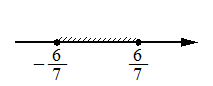
3) 

4) 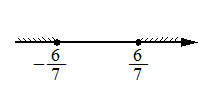
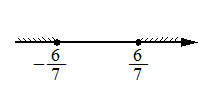
14
В ходе биологического эксперимента в чашку Петри с питательной средой поместили колонию микроорганизмов массой 10 мг. За каждые 30 минут масса колонии увеличивается в 3 раза. Найдите массу колонии микроорганизмов через 150 минут после начала эксперимента. Ответ дайте в миллиграммах.
Ответ:
15
В треугольнике ABC известно, что ∠BAC = 86°, AD – биссектриса. Найдите угол BAD. Ответ дайте в градусах.
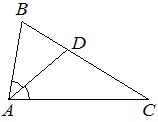 Ответ:
Ответ:
16
Радиус вписанной в квадрат окружности равен $$10\sqrt{2}$$. Найдите диагональ этого квадрата.
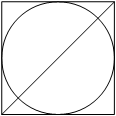 Ответ:
Ответ:
17
Сторона треугольника равна 14, а высота, проведённая к этой стороне, равна 23. Найдите площадь этого треугольника.
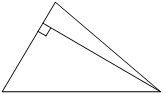 Ответ:
Ответ:
18
На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите длину его большей диагонали.
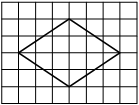 Ответ:
Ответ:
19
Какое из следующих утверждений верно? В ответ запишите номер выбранного утверждения.
1) Боковые стороны любой трапеции равны.
2) Серединные перпендикуляры к сторонам треугольника пересекаются в точке, являющейся центром окружности, описанной около треугольника.
3) Если две стороны и угол одного треугольника равны соответственно двум сторонам и углу другого треугольника, то такие треугольники равны.
20
Решите уравнение $$(x+4)^4-6(x+4)^2-7=0$$.
Ответ:
21
Теплоход проходит по течению реки до пункта назначения 176 км и после стоянки возвращается в пункт отправления. Найдите скорость течения, если скорость теплохода в неподвижной воде равна 19 км/ч, стоянка длится 1 час, а в пункт отправления теплоход возвращается через 20 часов после отплытия из него.
Ответ:
22
Постройте график функции$$y=\begin{cases}x^2-8x+14 \text{ при } x\geq 3,\\x-2 \text{ при } x<3.\end{cases}$$
Определите, при каких значениях m прямая y = m имеет с графиком ровно две общие точки.
Ответ:
23
Высота AH ромба ABCD делит сторону CD на отрезки DH = 24 и CH = 2. Найдите высоту ромба.
Ответ:
24
Через точку O пересечения диагоналей параллелограмма ABCD проведена прямая, пересекающая стороны AB и CD в точках E и F соответственно. Докажите, что отрезки AE и CF равны.
Ответ:
25
Углы при одном из оснований трапеции равны 47° и 43°, а отрезки, соединяющие середины противоположных сторон трапеции, равны 16 и 14. Найдите основания трапеции.
Ответ: