Главная / Тренировка
Тренировка
Тип 3 (из 24)
Тип 3 (из 24)
СПРАВОЧНЫЕ МАТЕРИАЛЫ
АЛГЕБРА
-
Формула корней квадратного уравнения:
$$x=\frac{-b\pm\sqrt{D}}{2a}\text{, где } D=b^2-4ac.$$
-
Если квадратный трёхчлен $$ax^2+bx+c$$ имеет два корня: $$x_1$$ и $$x_2$$, то
$$ax^2+bx+c=a(x-x_1)(x-x_2)$$;если квадратный трёхчлен $$ax^2+bx+c$$ имеет единственный корень $$x_0$$, то$$ax^2+bx+c=a(x-x_0)^2$$.
-
Абсцисса вершины параболы, заданной уравнением $$ax^2+bx+c$$ :
$$x_0=-\frac{b}{2a}.$$
-
Формула n-го члена арифметической прогрессии ($$a_n$$), первый член которой равен $$a_1$$ и разность равна $$d$$:
$$a_n=a_1+d(n-1)$$.
-
Формула суммы первых n членов арифметической прогрессии:
$$S_n=\frac{(a_1+a_n)n}{2}$$.
-
Формула n-го члена геометрической прогрессии $$b_n$$, первый член которой равен $$b_1$$, а знаменатель равен $$q$$:
$$b_n=b_1 \cdot q^{n-1}$$
-
Формула суммы первых $$n$$ членов геометрической прогрессии:
$$S_n=\frac{(q^{n}-1)b_1}{q-1}$$.
-
Формулы сокращенного умножения:
$$(a+b)^2=a^2+2ab+b^2$$;$$(a-b)^2=a^2-2ab+b^2$$;$$a^2-b^2=(a-b)(a+b)$$.
-
Свойства арифметического квадратного корня:
$$\sqrt{ab}=\sqrt{a}\cdot\sqrt{b} \text{ при } a\geq0, b\geq0$$;$$\sqrt{\frac{a}{b}}=\frac{\sqrt{a}}{\sqrt{b}} \text{ при } a\geq0, b>0$$.
-
Свойства степени при a>0, b>0
$$a^{-n} = \frac{1}{a^n}$$;$$a^n \cdot a^m = a^{n+m}$$;$$\frac{a^n}{a^m} = a^{n-m}$$;$$\Big(a^n\Big)^m = a^{nm}$$;$$(ab)^n = a^n \cdot b^n$$;$$\bigg(\frac{a}{b}\bigg)^n = \frac{a^n}{b^n}$$.
Таблица квадратов двузначных чисел
| Единицы | |||||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ||
Десятки | |||||||||||
| 1 | 100 | 121 | 144 | 169 | 196 | 225 | 256 | 289 | 324 | 361 | |
| 2 | 400 | 441 | 484 | 529 | 576 | 625 | 676 | 729 | 784 | 841 | |
| 3 | 900 | 961 | 1024 | 1089 | 1156 | 1225 | 1296 | 1369 | 1444 | 1521 | |
| 4 | 1600 | 1681 | 1764 | 1849 | 1936 | 2025 | 2116 | 2209 | 2304 | 2401 | |
| 5 | 2500 | 2601 | 2704 | 2809 | 2916 | 3025 | 3136 | 3249 | 3364 | 3481 | |
| 6 | 3600 | 3721 | 3844 | 3969 | 4096 | 4225 | 4356 | 4489 | 4624 | 4761 | |
| 7 | 4900 | 5041 | 5184 | 5329 | 5476 | 5625 | 5776 | 5929 | 6084 | 6241 | |
| 8 | 6400 | 6561 | 6724 | 6889 | 7056 | 7225 | 7396 | 7569 | 7744 | 7921 | |
| 9 | 8100 | 8281 | 8464 | 8649 | 8836 | 9025 | 9216 | 9409 | 9604 | 9801 | |
ГЕОМЕТРИЯ
- Сумма углов выпуклого n-угольника равна $$ 180^o (n-2) $$.
-
Средняя линия треугольника и трапеции
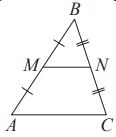
MN - ср. лин.MN || AC$$MN = \frac{AC}{2}$$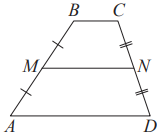
BC || ADMN - ср. лин.MN || AD$$MN = \frac{BC + AD}{2}$$ -
Описанная и вписанная окружности правильного треугольника
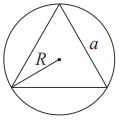
$$R = \frac{a\sqrt{3}}{3}$$$$S = \frac{a^2\sqrt{3}}{4}$$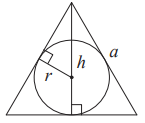
$$r = \frac{a\sqrt{3}}{6}$$$$h = \frac{a\sqrt{3}}{2}$$ -
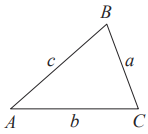
Для треугольника ABC со сторонами $$AB = c, AC = b, BC = a$$:$$\frac{a}{sinA} = \frac{b}{sinB} = \frac{c}{sinC} = 2R$$,где R – радиус описанной окружности.
Для треугольника ABC со сторонами $$AB = c, AC = b, BC = a$$:$$c^2 = a^2 + b^2 - 2ab\cos{C}$$. -
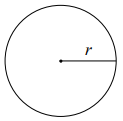
Длина окружности $$С = 2\pi r$$Площадь круга $$S = \pi r^2$$
-
Параллелограмм
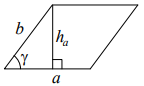
$$S=ah_a$$$$S=ab\sin{\gamma}$$Треугольник
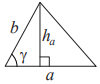
$$S=\frac{1}{2}ah_a$$
$$S=\frac{1}{2}ab\sin{\gamma}$$ -
Трапеция
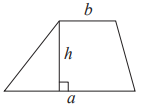
$$S=\frac{a+b}{2}\cdot h$$Ромб
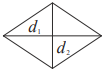
$$d_1, d_2$$ - диагонали$$S=\frac{1}{2}d_1d_2$$ -
Прямоугольный треугольник
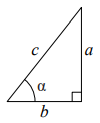
$$\sin{\alpha} = \frac{a}{c}$$
$$\cos{\alpha} = \frac{b}{c}$$
$$tg\alpha = \frac{a}{b}$$ - Теорема Пифагора: $$a^2 + b^2 = c^2$$
- Основное тригонометрическое тождество: $$\sin^2{\alpha} + \cos^2{\alpha} = 1$$
-
Некоторые значения тригонометрических функций
$$\alpha$$ градусы 0o 30o 45o 60o 90o 180o 270o 360o $$sin{\alpha}$$ 0 $$\frac{1}{2}$$ $$\frac{\sqrt{2}}{2}$$ $$\frac{\sqrt{3}}{2}$$ 1 0 -1 0 $$cos{\alpha}$$ 1 $$\frac{\sqrt{3}}{2}$$ $$\frac{\sqrt{2}}{2}$$ $$\frac{1}{2}$$ 0 -1 0 1 $$tg{\alpha}$$ 0 $$\frac{\sqrt{3}}{3}$$ 1 $$\sqrt{3}$$ - 0 - 0